Новая теория может помочь астрономам найти планеты-гиганты во Вселенной

Июн 22, 2023 Леонид Гляделов

Исследователи из Нотр-Дам разработали концепцию, которая может быть использована для прогнозирования наличия крупных планет во внешних регионах экзопланетной системы.

Маттиас Хе и Лорен Вайс создали теорию, которая была загружена на сервер arXiv и основана на смешении двух наборов данных.

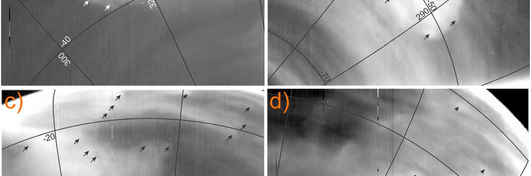
Исследователи в области астрономии используют два основных метода обнаружения планет — транзиты и записи радиальных скоростей (RV). До недавнего времени данные, полученные при изучении транзитных экзопланет, и данные, собранные с помощью RV, хранились отдельно, что создавало значительный пробел в знаниях астрономов о том, как эти два подхода будут интерпретировать одну и ту же систему.

Кеплеровский обзор планет-гигантов, проект, осуществленный учеными из Нотр-Дам, объединил данные Кеплера и Кека для исследования 63 различных экзопланетных систем. Из 177 планет, включенных в выборку, большинство были впервые обнаружены благодаря транзитам, но около 20 из них были идентифицированы с помощью измерений радиальной скорости.

Изучив объединенные наборы данных, ученые исследовали потенциальные контрольные маркеры, которые могут указывать на существование крупной планеты в более отдаленной области экзопланетной системы.

Было установлено, что корреляция статистически значима по отношению к менее признанному индексу сложности разрыва, который определяет, насколько разнообразно орбиты планет расположены друг от друга. В системе с низкой сложностью планеты располагаются эквидистантно, в то время как в системе с высокой сложностью их позиции разбросаны. Ученые определили, что большая сложность резко повышает вероятность существования гигантской планеты во внешней части нашей Солнечной системы, которую можно обнаружить с помощью методов RV, но не с помощью транзита.

Этот метод имеет недостаток в том, что для точного расчета можно использовать только четыре системы — все с тремя внутренними планетами. Тем не менее, исследователи обнаружили, что те же самые рассуждения справедливы при учете газового гиганта в расчете сложности, даже если во внутренней Солнечной системе присутствуют только две планеты.